|
4.3.4 - Condizioni di indifferenza
Quando esistono alcune combinazioni delle variabili di ingresso che sappiamo non si presenteranno mai, si possono aggiungere nelle equazioni delle uscite alcuni o tutti i termini relativi alle suddette combinazioni.
Questo lo si fa per poter poi minimizzare ulteriormente le espressioni e lo si può fare perché in corrispondenza di tali configurazioni, che in realtà non si avvereranno mai, la funzione può assumere indifferentemente valore 0 oppure 1.
Nella mappa di Karnaugh tali configurazioni si indicano con un segno particolare e sono molto utili per la semplificazione della funzione stessa a seconda di quanto sia più utile la loro considerazione come 1 o come 0.
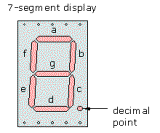
Se ad esempio si volesse scrivere l’espressione che rappresenta uno dei 7 segmenti luminosi che formano, in un display digitale, ciascuna cifra per la rappresentazione di una cifra da 0 a 9, utilizzando la mappa di Karnaugh si utilizzerebbe la seguente procedura.
Per poter rappresentare le cifre da 0 a 9, cioè tutte quelle rappresentabili su un display digitale, abbiamo bisogno di 4 variabili (A,B,C,D) per un totale di 24 = 16 combinazioni.
Rappresentiamo la tabella di verità delle possibili combinazioni:
|
A
|
B
|
C
|
D
|
Numero
rappresentato
|
U
|
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
0
|
1
|
1
|
1
|
|
0
|
0
|
1
|
0
|
2
|
0
|
|
0
|
0
|
1
|
1
|
3
|
1
|
|
0
|
1
|
0
|
0
|
4
|
1
|
|
0
|
1
|
0
|
1
|
5
|
1
|
|
0
|
1
|
1
|
0
|
6
|
1
|
|
0
|
1
|
1
|
1
|
7
|
1
|
|
1
|
0
|
0
|
0
|
8
|
1
|
|
1
|
0
|
0
|
1
|
9
|
1
|
|
1
|
0
|
1
|
0
|
[10]
|
|
|
1
|
0
|
1
|
1
|
[11]
|
|
|
1
|
1
|
0
|
0
|
[12]
|
|
|
1
|
1
|
0
|
1
|
[13]
|
|
|
1
|
1
|
1
|
0
|
[14]
|
|
|
1
|
1
|
1
|
1
|
[15]
|
|
In particolare si vuole scrivere la funzione U in grado di poter rappresentare l’utilizzo di uno dei 7 segmenti luminosi che formano la cifra digitale, ad esempio il segmento “c” nella seguente figura:
Rappresentiamo la mappa di Karnaugh in grado di minimizzare la funzione U che si vuole trovare:
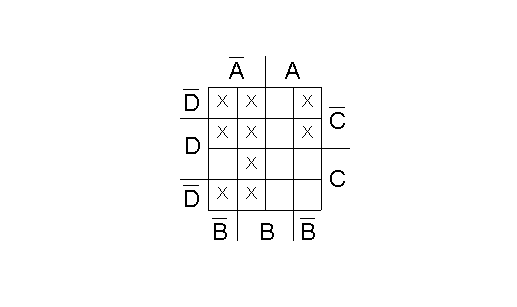Nell’esempio appena rappresentato le combinazioni delle variabili di ingresso relative ai numeri decimali 10, 11, 12, 13, 14, 15 non verranno mai realizzate per limitazione della funzione che si vuole realizzare.
Dalla tabella di verità possiamo ottenere le espressioni logiche di tali combinazioni che riportiamo, con il simbolo del quadratino, sulla mappa di Karnaugh; considerando ”1” alcune di queste combinazioni, si riesce a minimizzare ulteriormente la funzione ricercata:
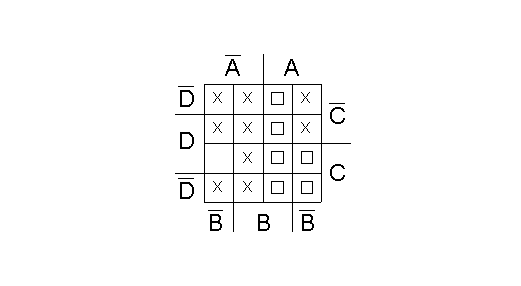Applicando le regole fondamentali che consentono una ulteriore semplificazione della mappa, in particolare le regole che permettono di raggruppare i quadratini adiacenti, si può finalmente scrivere la funzione che soddisfa le nostre richieste:
F = B + C' + D'
50/53
|
