4.3.3  - Mappe di Karnaugh

[I1] [I2] [I3] [E1] [E2] [F1] [F2] [F3] [ES1] [ES2]

Nella Mappa di Karnaugh ogni casella deve rappresentare una delle 2ⁿ combinazioni delle n variabili che compaiono nella funzione da minimizzare, quindi è possibile, attraverso la tabella della verità, individuare sulla mappa quali siano le caselle corrispondenti ai singoli termini.

Ad esempio, la funzione

f = A∙B∙C∙D + A∙B + A'∙B'∙C'∙D +A'∙B'∙C∙D' + A'∙B'∙C'∙D'

contiene 4 variabili A, B, C, D, quindi le combinazioni saranno 2⁴ = 16. La mappa dovrà allora contenere 16 caselle.

La mappa inoltre deve avere forma tale che per ogni variabile il numero dei quadratini interni deve essere divisibile in due parti uguali; in una parte sono considerati i termini che contengono quelle variabili in forma diretta, sull’altra parte i termini che contengono le stesse variabili in forma negata.

La mappa a 4 variabili può assumere la seguente forma:

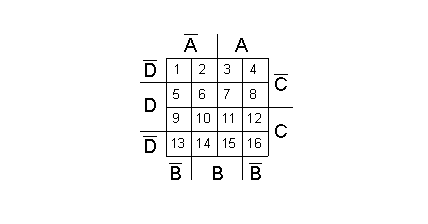Si abbia da collocare nella mappa il primo termine della funzione scritta sopra, cioè A∙B∙C∙D.

Esso contiene A perciò può essere uno qualsiasi dei quadratini indicati con i numeri 3, 4, 7, 8, 11, 12, 15, 16.

Poi contiene B: quindi limitiamo ulteriormente i quadratini possibili a 3, 7, 11, 15.

Contiene C: dobbiamo perciò ancora scartare i quadratini 3 e 7.

Infine contiene D e si deve perciò scartare il quadratino 15. Allora il quadratino 11 rappresenta il termine A∙B∙C∙D.

Consideriamo il termine A∙B; con un ragionamento analogo al precedente vediamo che esso è rappresentato dall’insieme dei quadratini 3, 7, 11, 15.

Il termineA'∙B'∙C'∙D è rappresentato dal quadratino 5.

Il termine A'∙B'∙C∙D' è rappresentato dal quadratino 13.

Il termine A'∙B'∙C'∙D' è rappresentato dal quadratino 1.

Possiamo rappresentare graficamente sulla mappa l’intera funzione f; essa risulta essere l’insieme dei quadratini segnati con una X nella seguente mappa:

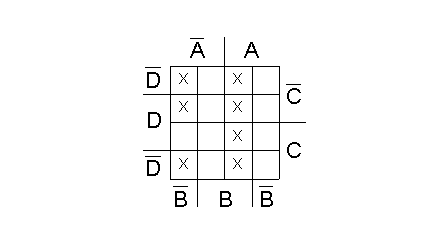Vi sono tre considerazioni fondamentali che permettono la semplificazione della funzione:

1. Se i quadratini relativi ad un termine sono contenuti nei quadratini relativi ad un termine più grande, il primo termine può essere eliminato.
   Nel nostro caso:
   A∙B∙C∙D + A∙B = A∙B ∙ (C∙D + 1) = A∙B
   (casella 11 contenuta nell’insieme delle caselle 3-7-11-15)
   Quindi il termine A∙B∙C∙D si può eliminare.

2. Se due termini hanno i quadratini che li rappresentano adiacenti fra loro sulla mappa, si possono riunire per formare un unico termine in cui è stata eliminata la variabile che compare in forma diretta nell’una e negata nell’altra.
   Nel nostro caso consideriamo i termini:
   A'∙B'∙C'∙D + A'∙B'∙C'∙D' = A'∙B'∙C'∙ (D +D') = A'∙B'∙C' ( caselle 1-5 conglobate )
   e inoltre A'∙B'∙C∙D' + A'∙B'∙C'∙D' = A'∙B'∙D'∙ (C +C') = A'∙B'∙D' ( casella 1 )

3. Se tre termini hanno i quadratini che li rappresentano adiacenti tra loro ( come nel caso riportato sotto ) si possono riunire a formare due soli termini aventi una parte in comune.
   Ad esempio ai tre termini:
   A'∙B'∙C'∙D + A'∙B'∙C'∙D' + A'∙B'∙C∙D'
   Per la nota relazione che A + A = A, possiamo aggiungere un termine uguale ad uno qualunque dei tre, senza che la funzione cambi; possiamo perciò avere:
   A'∙B'∙C'∙D + A'∙B'∙C'∙D' + A'∙B'∙C'∙D' + A'∙B'∙C∙D'
   che è uguale alla funzione scritta sopra (avendo aggiunto il termine A'∙B'∙C'∙D' già presente).
   Si ricava:
   A'∙B'∙C'∙D + A'∙B'∙C'∙D' + A'∙B'∙C'∙D' + A'∙B'∙C∙D' = A'∙B'∙C'∙ (D +D') + A'∙B'∙D'∙ (C +C') = A'∙B'∙C' + A'∙B'∙D'
   Quindi sulla mappa le caselle 1-5 e 1 possono essere conglobate nelle due caselle 1-5, come già visto al punto 2.

Occorre infine osservare che:

• Si possono considerare adiacenti anche due termini giacenti agli estremi di una stessa riga (orizzontale) o colonna (verticale) di quadratini.
  Ad esempio, nella prima mappa di Karnaugh rappresentata, le caselle 5 e 8, oppure 4 e 16, sono adiacenti. Ciò significa che la mappa può essere considerata come lo sviluppo della superficie laterale di un cilindro per cui i due lati opposti sono sovrapposti.

• La funzione di minimo costo è una delle somme non ridondanti, cioè che ha il minor numero di quadratini comuni a diversi termini (come la casella 1) nei conglobamenti eseguiti secondo il precedente punto 3.

   49/53   

Approfondimenti/commenti:

Nessuna voce inserita

Inserisci approfondimento/commento