Si ha quando la congiunzione “o” ( + ) lega più variabili in modo che la funzione sia vera (1) quando almeno una o entrambe le variabili sono vere (1).
L’operatore OR si rappresenta mediante una lampada F che viene alimentata attraverso due interruttori A e B in parallelo come in figura seguente. La lampada si accende in seguito alla chiusura di uno qualunque dei due interruttori; in altre parole la lampada è accesa se si chiude l’interruttore A o (OR) il B.
Quanto affermato si può esprimere con la relazione:
F = A + B
dove F è la funzione “accensione” che si vuole determinare, ed A e B sono le variabili o stato degli interruttori A e B.
Se poniamo:
interruttore chiuso = 1 ALLORA lampada accesa = 1
interruttore aperto = 0 ALLORA lampada spenta = 0
dalla relazione F = A + B si possono dedurre i seguenti postulati:
1 + 1 = 1
che corrisponde al fatto che se si chiudono entrambi gli interruttori (A = B = 1) allora la lampada si accende (F = 1). Inoltre:
1 + 0 = 1
0 + 1 = 1
cioè se si chiude un solo interruttore (A = 1 e B = 0 o viceversa), anche in questi casi, la lampada si accende (F = 1). Infine:
0 + 0 = 0
se si aprono entrambi gli interruttori (A = B = 0) la lampada si spegne (F = 0).
Ne deriva quindi la seguente Tabella della verità [I1]:
|
A |
B |
F |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Il simbolo grafico usato per indicare il blocco logico OR, e quindi il simbolo grafico usato per indicare l’espressione booleana A + B = F, è il seguente:
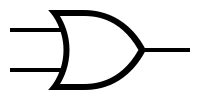
Anche la funzione OR gode sia della proprietà commutativa [I2] che della proprietà associativa [I3], in particolare:
Per la proprietà commutativa risulta:
A + B = B + A
Per la proprietà associativa risulta:
A + B + C = A + (B + C) = (A + B) + C