|
- I Satelliti artificiali -
Introduzione
Per lanciare un satellite è necessario che questi sia abbinato ad un vettore, solitamente un razzo veicolante, capace di lasciare l’atmosfera terrestre. La condizione detta di fuga, e che esso abbia una velocità, tale da consentirgli di vincere la forza gravitazionale,[I1]
[I2]
[I3]
[E1]
[E2]
[E3]
[F1]
[F2]
[F3]
[S1]
[S2] che sia pari ad almeno 11200 m /sec.
Il primo satellite artificiale fu messo in orbita dall’URSS nel 1957 ad esso venne dato il SPUTNIK.
Periodo di rivoluzione dei satelliti
I satelliti artificiali descrivono un’orbita situata su un piano passante per il centro della Terra ed immobile rispetto alle stelle, comportandosi come i pianeti intorno al Sole e la Luna intorno alla Terra.
Per i satelliti artificiali valgono le leggi di Keplero, pertanto avremo che l’orbita descritta dal satellite artificiale, in relazione al semiasse dell’ellittica,[I1]
[E1][S1] sarà regolato dalla seguente relazione:
K = a³ / T²;
con K costante di Keplero;
a semiasse maggiore dell'orbita;
T periodo di rivoluzione.
Supponendo l’orbita circolare avremo r = a e per le leggi della dinamica m v²/ r =G M m / r²
ovvero la forza centrifuga deve eguagliare la forza gravitazionale.
Con M massa terrestre, “m” massa satellite, G costante universale gravitazionale.
Dalla relazione che lega la velocità tangenziale a quella angolare avremo:
ω = √ (G M / r³ ) segue T = 2 π √ (r³ / G M) ;
G = 6,67 10-¹¹ m³ / kg s
[E1]
[E1]
[F1]
[F2] M = 5,972245 1024 kg.
Nota per “r” si intende il raggio condotto tra i baricentri della Terra e del satellite avremo quindi che r = Rt + h, con Rt raggio terrestre pari a 6371 Km e “h” quota dell’orbita dalla superficie terrestre, variabile a seconda del tipo del satellite.
Coordinate altazimutali di un corpo celeste
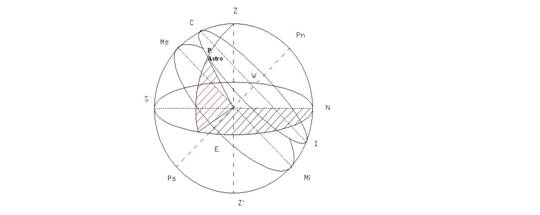Per esprimere le coordinate altazimutali[I1]
[I2]
[I3]
[E1]
[F1]
[S1]
di un corpo sulla sfera celeste si fissano dapprima due cerchi massimi secondo i criteri seguenti.
Il cerchio massimo, ottenuto tra l’intersezione del piano contenete lo zenit Z e il nadir Z’ ed i poli celesti Pn e Ps, è detto meridiano celeste. Il meridiano celeste si divide in due semicerchi detti rispettivamente meridiano superiore quello contenente il polo nord o anche verticale nord e meridiano inferiore l’altro, i due semicerchi sono tagliati dall’equatore celeste nei punti mezzo cielo superiore Ms e mezzo cielo inferiore Mi, mentre a loro volta incontrano l’orizzonte astronomico sulla sfera celeste in due punti N - S. Il verticale ortogonale al meridiano celeste, incontra l'orizzonte astronomico sulla sfera celeste in due punti detti E - W. Il cerchio base è rappresentato dal cerchio massimo ortogonale alla verticale dell’osservatore ovvero l’orizzonte astronomico. Si definisce azimut l’arco di orizzonte astronomico percorso in senso orario tra 0 ° e 360 ° compreso tra la verticale nord e l’astro di riferimento. Mentre l’arco, della verticale passante per l’astro, compreso tra l’orizzonte astronomico e l’astro esprime l’altezza, essa è compresa tra pari a 0° e 90° + 90° verso il Pn nord e negativa - 90° verso il Ps.
Parametri orbitali satellitari
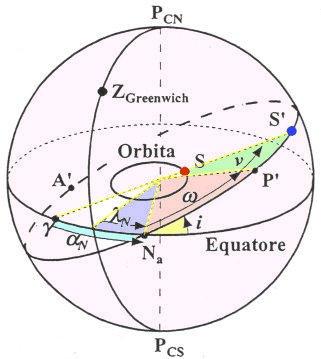Come in astronomia, anche per i satelliti per individuare la loro posizione nello spazio occorrono i seguenti sei parametri orbitali: [I1]
[E1]
[S1]
a semiasse maggiore dell'orbita;
e eccentricità dell'orbita. E’uguale a zero se circolare;
t0 istante del passaggio del satellite dal perigeo, – al perigeo si ha la minima distanza satellite Terra -;
αN ascensione retta del nodo ascendente. Longitudine del nodo ascendente*, contata nel piano equatoriale a partire dal punto γ (equinozio di primavera);
i inclinazione del piano orbitale rispetto al piano dell'equatore celeste. L’angolo va contato con vertice il nodo ascendente, da 0° a 180°, in senso antiorario dall'equatore verso l’orbita;
ω argomento del perigeo, ossia l'angolo, nel piano dell'orbita, fra la direzione del nodo ascendente e la direzione del perigeo.
La posizione dell'orbita rispetto al meridiano di Greenwich si ottiene calcolando la longitudine terrestre λ N del nodo ascendente mediante la seguente relazione :
λ N =αN – Ts; dove Ts rappresenta il tempo siderale riferito al primo meridiano.
* Sono definiti nodi i due punti intersezione dell’equatore terrestre con il cerchio massimo ottenuto dall’intersezione del piano contenente l’orbita satellitare, con la sfera terrestre. Il nodo detto ascendente è quello che s’incontra percorrendo il cerchio massimo tra l’emisfero sud e Nord,. Mentre il nodo incontrato nel percorrere il cerchio massimo tra l’emisfero Nord e Sud è detto nodo discendente.
Perturbazioni dell'orbita
L'orbita di un satellite subisce diverse perturbazioni causate principalmente :
1) Dalla forma non perfettamente sferica della Terra e dalla non uniforme distribuzione della sua massa;
2) Dalla presenza di altri corpi celesti, in particolare Sole e Luna;
3) Dall'attrito con l'atmosfera terrestre (aerodynamic drag);
4) Dalla pressione esercitata dalla radiazione solare.
L'attrito con l'atmosfera varia notevolmente con la quota e produce una perdita di energia cinetica che si traduce in una perdita di quota ad ogni giro. La traiettoria satellitare ha bisogno di opportuni interventi correttivi senza dei quali diventerebbe una specie di spirale ellittica, portando gradualmente al collasso il satellite verso la Terra. Il tempo di collasso è legato al semiasse orbitale. Maggiore è il semiasse e maggiore è il tempo impiegato nel compiere la spirale. Quando il satellite raggiunge l’atmosfera terrestre si disintegra, data l’alta velocità con la quale impatta.
Per ovviare a tale problemi i satelliti sono dotati di almeno due razzi ad idrazina, uno per la spinta radiale ed un altro per quella tangenziale, che ne consentono attraverso opportuni sofisticati sistemi di controllo da terra il loro avviamento e la durata della spinta, garantendo il rispetto della traiettoria programmata. Resta da dire che per ogni satellite esiste un inevitabile ciclo di vita, che è legato alle riserve di propellente, terminate le quali, i satelliti non possono avere correzioni orbitali collassano presto o tardi sulla Terra.
Un analogo effetto, anche se molto più piccolo, è prodotto dalla radiazione solare sui satelliti di grandi dimensioni.
3/7
|
