|
- Le Coordiante cartesiane e polari -
Terna di riferimento
A questo punto non rimane che definire una terna di riferimento per l'osservatore e per il satellite. Scegliamo le terne cartesiane di riferimento X,Y,Z e x,y,z, entrambe con origine il centro della Terra. Per l'osservatore sia dato il seguente riferimento: l'asse z diretto lungo l'asse dei poli verso il polo nord, l'asse x nel piano equatoriale diretto lungo il meridiano di Greenwich e l'asse y perpendicolare agli assi x e z. Tale terna è nota come terna ECEF (Earth Centered. Earth Fixed).[I1] .[I2] Per il satellite definiremo : asse X diretto verso il perigeo, asse Z perpendicolare al piano dell'orbita, asse Y perpendicolare ad X e Z.
Coordinate cartesiane e geografiche
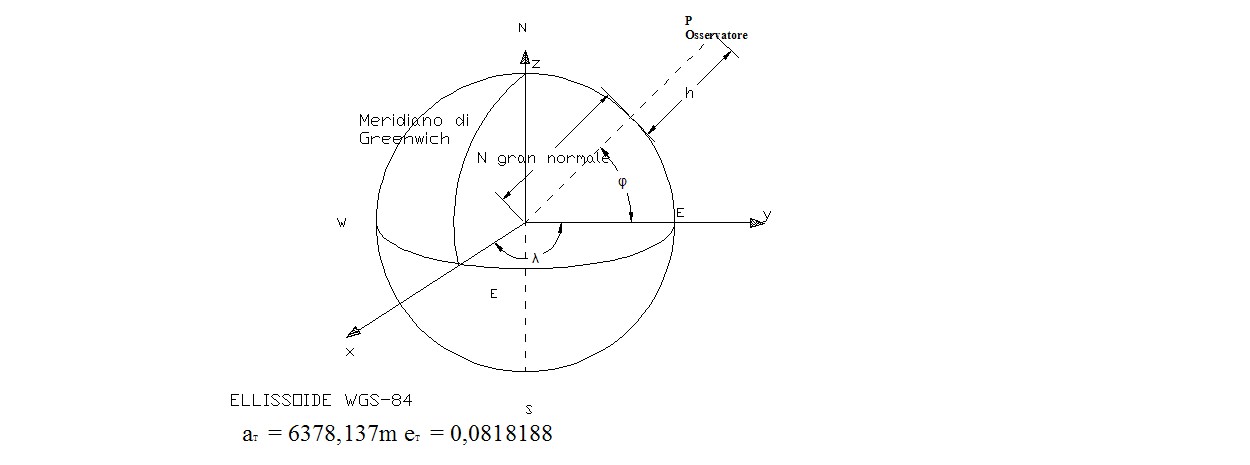Le coordinate cartesiane del generico punto per un osservatore ad un’altezza h sulla verticale terrestre saranno date dalle equazioni delle coordinate geografiche :[F1] [S1]
x = (N +h) cos φ cos λ
y = (N +h) cos φ sin λ
z= [N ( 1 – eT ² ) + h] sin φ
con N = aT / ( √ ( (1 – eT ²) sin² φ) ) ;
[E1]
[E1]
[F1]
[F2]
Determinazione delle coordinate cartesiane del satellite
La figura seguente, rappresenta il sistema di
riferimento spaziale per le coordinate satellitari ( X, Y, Z). La figura riporta anche il sistema di coordinate spaziali per l'osservatore (x, y, z ). Per entrambi è stata scelta l'origine degli assi coincidente con il centro della Terra, in maniera di avere un riferimnmeto di coordiante unico a cui riferire l'osservatore ed il satellite.
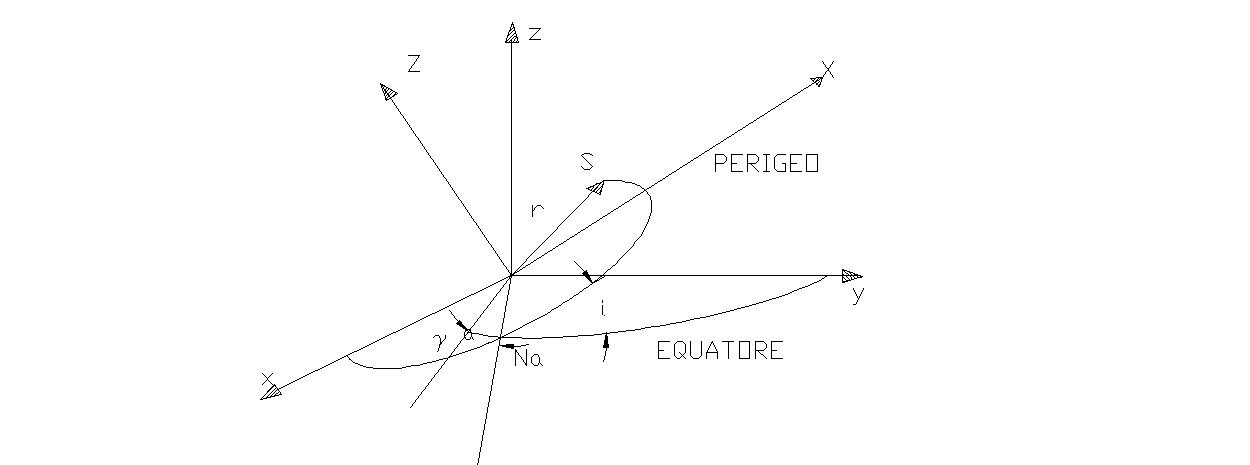Le relazioni che seguono, determinano le cordinate Satellitari X,Y,Z note le coordinate polari.
X = r cos ø;
Y = r sin ø;
Z = ;
coordinate polari calcolate a partire dai dati di posizione orbitali r,ø. Con r distanza misurata dal centro della Terra al baricentro del satellite, e ø angolo di rotazione compiuto in senso orario da 0° a 360°. Lo zero angolare si ha quando r giace sull'asse x nel verso positivo. [I1]
[E1]
[F1]
[S1]
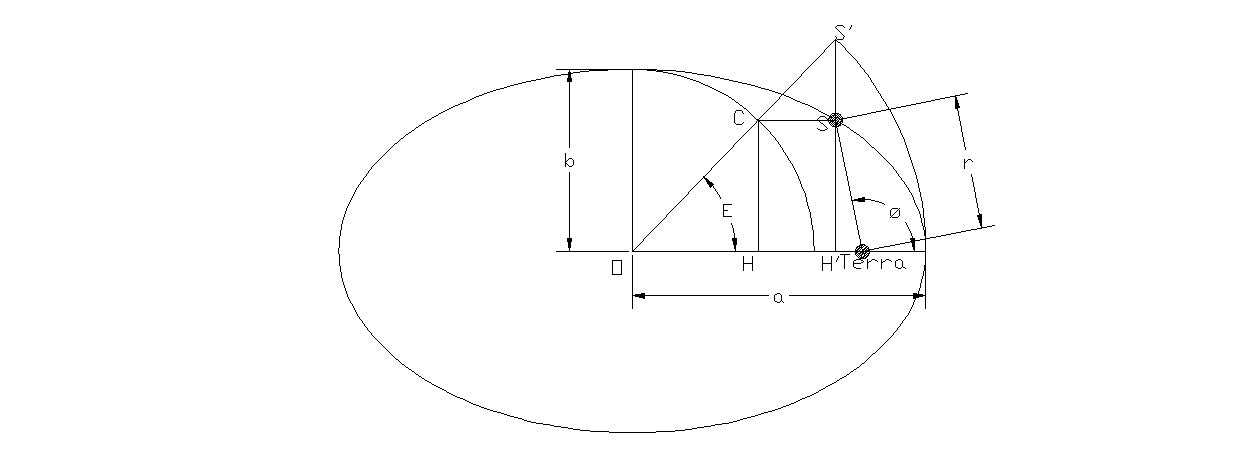Dove r = a ( 1- e cos E) ;
tan ø = √ (1- e²) (sin E / (cos E – e)) ;
con E anomalia eccentrica ottenuta dall’equazione di Keplero,[S1][S2]
M = E – e sin E, nota l’anomalia media, M = n (t – to); con t – to = intervallo di tempo calcolato a partire dal passaggio al perigeo ed n = 2π / T ;
T periodo medio orbitale.
Procedendo con una rotazione degli assi in senso orario si hanno le trasformazione di coordinate seguenti:
rotazione di un angolo ω attorno all’asse Z, portando l’asse X in sovrapposizione della linea dei nodi con verso al Nodo ascendente;
rotazione intorno al nuovo asse X di un angolo i, ottenendo la sovrapposizione dell’orbita sul piano equatoriale ;
rotazione dell’asse Z sul piano equatoriale sovrapponendo la linea dei nodi all’asse x uscente dal meridiano di Greenwich. Questa trasformazione è legata alla velocità di rotazione terrestre secondo la relazione λ N =aN – Ts; (vedi sopra).
Si perviene alle seguenti relazioni delle coordinate satellitari:
xi = r [cos (ω + ø ) cos λ N – sin (ω + ø ) sin λ N cos i ];
yi = r [cos (ω + ø ) sin λ N + sin (ω + ø ) cos λ N cos i ];
zi = r sin (ω + ø ) sin i;
4/7
|
