|
- La Terra-
Il Geoide
Il pianeta Terra non è una superficie geometrica e la sua rappresentazione matematica dà origine al Geoide [I1] [I2] [E1] [E2] [F1][F2][S1][S2]Essendo la Terra per circa i ¾ della sua superficie ricoperta da acqua, il cui livello medio della superficie è regolare mentre la restante parte è un’estensione di pianure e rilievi montuosi, se in astratto si immagina di prolungare il livello medio dei mari attraverso i continenti, si ottiene il Geoide. Il Geoide non è una figura geometrica ma una rappresentazione matematica della superficie terrestre mediante una superficie convessa in ogni suo punto.
L'ellissoide
Il Geoide è approssimabile ad un ellissoide, ovvero alla figura geometrica ottenuta dalla rotazione su se stesso del semiasse minore dell’ellisse. Il semiasse di rotazione dell’ellisse è scelto in modo tale da rappresentare al meglio la superficie del geoide, pertanto il semiasse minore ed il centro di rotazione sono scelti in modo da coincidere con il baricentro e l’asse di rotazione del geoide. I semiassi terrestri sono rispettivamente di: 6.357 Km quello minore, e di 6.378,5 Km quello maggiore. L’ellissoide [I1] [I2] [E1] [F1] [S1] terrestre è caratterizzato dal diametro polare pari a 12.714 Km e da quello equatoriale pari a 12.757 Km. Il rapporto, in valore assoluto, tra la differenza dei diametri rapportata al diametro equatoriale esprime l’ellitticità della Terra che è pari a 1/297 . Ai fini pratici, in considerazione dell’ellitticità terrestre la Terra viene considerata una sfera con il raggio pari a 6.371,2 Km, scelto in modo tale da avere la stessa superficie del geoide.
I meridiani ed i paralleli
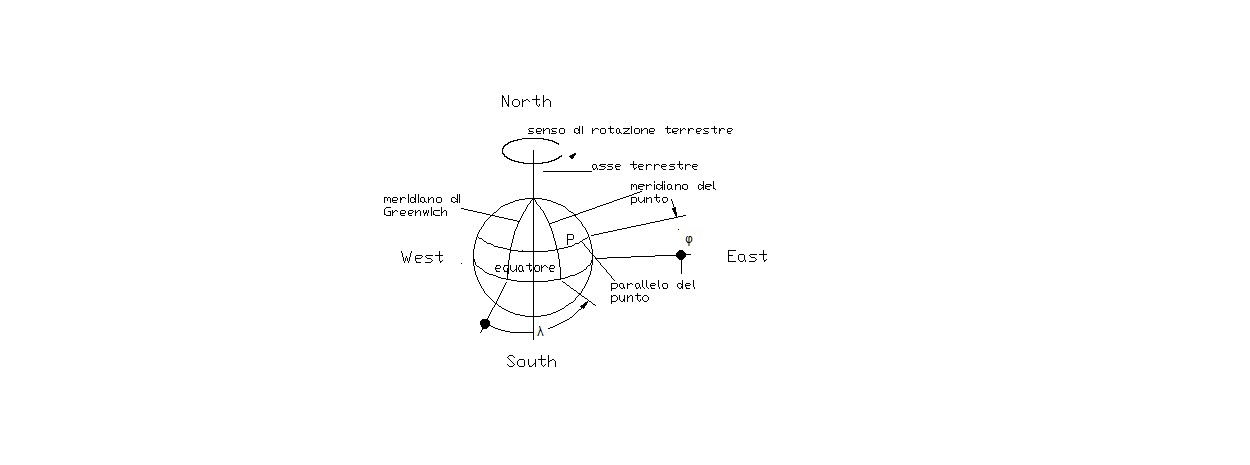
Approssimando la Terra con una sfera, il cui asse dei poli sia parallelo all’asse di rotazione terrestre del geoide, ogni punto della sfera conserverà le coordinate del geoide. L’asse di rotazione incontra la sfera terrestre in due punti detti rispettivamente polo nord (north) e polo sud (south). Un osservatore posto al polo nord vede la Terra ruotare sotto di se in senso antiorario. Prendendo a riferimento la rotazione introno all’asse terrestre, avremo che, se partendo da un punto sulla Terra per raggiungerne un altro compiremo uno spostamento concorde con la rotazione terrestre, il punto di partenza sarà ad ovest (west) rispetto al punto d’arrivo. Viceversa un punto sulla Terra sarà ad est (east) di un altro, quando partendo dal primo per raggiungere il secondo compiremo uno spostamento opposto alla rotazione terrestre. I piani che tagliano la Terra perpendicolarmente all’asse terrestre determinano un circonferenza su di essa, quando il piano passa per il centro della Terra la circonferenza ottenuta è un cerchio massimo, ovvero un cerchio avente lo stesso raggio della sfera. Il cerchio massimo perpendicolare all’asse terrestre è detto equatore, il piano che lo determina taglia la sfera in due semisfere dette rispettivamente emisfero boreale o nord quello che contiene il corrispondente polo ed emisfero sud o boreale l’altro.
I piani passanti per l’asse di rotazione tagliano la sfera dando luogo sempre a cerchi massimi. Considerando un osservatore sulla sfera terrestre, la parte del semicerchio massimo compreso tra i poli è detto meridiano, il semicerchio opposto, e quindi non visibile all’osservatore, è detto antimeridiano. E’ opportuno notare che in relazione al punto dell’osservatore il meridiano è anche antimeridiano del meridiano opposto.
Le coordinate geografiche
Un punto sulla sfera terrestre è determinato mediante due grandezze, rappresentati rispettivamente la distanza angolare dell’equatore al parallelo del punto, detta latitudine ( φ ), e la seconda anch’essa rappresentante la distanza angolare dal meridiano di riferimento ovvero quello di Greenwich, ed il meridiano del punto, detta longitudine( λ ). Avremo che la latitudine sarà compresa tra 0° e 90° dall’equatore al polo rispettivamente nord o sud, e per la longitudine tra 0° e 180° rispettivamente est ed ovest. [F1] [F2][S1] Per esempio le coordinate della città di Torino sono latitudine 45° 10’ N longitudine 7° 40’ E.
1/7

|