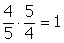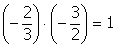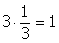Il prodotto di due numeri razionali espressi in forma frazionaria è il numero espresso dalla frazione che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denominatori.
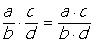
Esempio:
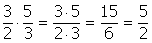
Anche in Q, come in Z, la moltiplicazione è un'operazione interna e valgono le medesime proprietà (commutativa, associativa, distributiva rispetto all'addizione, esistenza dell'elemento neutro 1, legge di annullamento del prodotto).
Per la moltiplicazione in Q vale anche una proprietà analoga all'esistenza dell'opposto nell'addizione.
Si dice reciproco o inverso di un numero razionale espresso in forma frazionaria a/b il numero espresso dalla frazione b/a, ottenuta scambiando numeratore e denominatore.
Poiché non esistono frazioni con denominatore 0, il numero 0 non ha reciproco.
Esempi:
Il reciproco di 2/3 è 3/2.
Il reciproco di 5/7 è 7/5.
Il reciproco di 3 è 1/3.
In Q vale dunque questa nuova proprietà, detta esistenza dell'inverso (o reciproco):
di ogni numero razionale, escluso lo 0, esiste il reciproco; il prodotto di un numero per il suo reciproco è sempre uguale all'elemento neutro della moltiplicazione (cioè 1).
Esempi: