|
I numeri razionali - Frazioni e numeri decimali
Definizioni:
Si dicono numeri decimali quei numeri che presentano, nel loro sviluppo decimale, cifre
alla destra di quella delle unità.
[ES1]
[ES2]
Si dice numero decimale limitato un numero decimale avente un numero finito di cifre dopo la virgola.
[I1]
[I2]
Si dice numero decimale illimitato periodico un numero decimale la cui parte dopo la
virgola, da una certa cifra in poi, è formata da un gruppo di cifre detto periodo che si ripete indefinitamente.
[I1]
Un numero decimale periodico è detto semplice se il periodo inizia subito dopo la virgola;
è detto misto se presenta un gruppo di cifre comprese tra la virgola e il periodo. Tale
gruppo di cifre è detto antiperiodo.
[I1]
Una frazione, in base alla definizione data nei paragrafi precedenti, può essere rappresentata
come numero decimale dal quoziente della divisione del numeratore per il denominatore.
In base alla proprietà invariantiva, possiamo concludere che frazioni tra loro equivalenti
danno luogo allo stesso numero decimale.
Eseguendo la divisione tra numeratore e denominatore, possono presentarsi due casi:
la divisione termina dopo un numero finito di passaggi e dà come resto 0 e come quoziente un
numero decimale limitato.
Esempio:
13:5 = 2,6
la divisione non termina, in quanto da un certo punto in poi inizia a ripetersi uno stesso resto
diverso da 0. In questo caso la frazione dà luogo ad un numero decimale illimitato
periodico.
Esempio:
11:3 = 3,(6)
dove si è utilizzata la convenzione di indicare il periodo fra parentesi tonde.
In generale, una frazione ridotta ai minimi termini dà luogo a:
un numero decimale limitato quando il suo denominatore ha come divisori primi solo i
divisori primi di 10, ossia 2 o 5;
un numero decimale illimitato periodico quando il suo denominatore ha almeno un divisore
primo diverso da 2 e 5.
Esempi:
13/20 = 0,65
4/15 = 0,266666666666…
Consideriamo una frazione m/n ridotta ai minimi termini. Siccome nella divisione del numeratore
per il denominatore i resti parziali, ossia quelli che si ottengono nei successivi passi della
divisione devono sempre essere minori del divisore, essi devono essere minori o uguali a
n-1. Allora, dopo un certo numero di passi, escludendo il caso che si presenti come resto 0
(in tal caso la divisione si arresterebbe dando luogo ad un numero decimale limitato), dovrà
ricomparire un resto già ottenuto in precedenza e, con esso, ricomparire la stessa cifra nel
quoziente. Da quel punto in poi tutta loperazione si ripete periodicamente. Dunque, il massimo
numero di cifre del periodo è n-1.
[F1].
Per quanto riguarda il problema inverso, ossia il passaggio da un numero decimale ad una sua
frazione generatrice, si può dire che tale problema ammette soluzione se e solo se il numero
decimale è limitato oppure periodico.
[ES1]
.
In particolare:
dato un numero decimale limitato, una sua frazione generatrice è quella che si ottiene
moltiplicando e dividendo il numero per una potenza di dieci avente esponente uguale al numero di
cifre dopo la virgola del decimale dato.
Esempio:
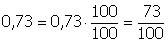
dato un numero decimale illimitato periodico, per calcolare una sua frazione generatrice occorre:
scrivere il numero senza la virgola e senza il periodo:
8,(5) ---> 85
sottrarre dal numero tutto ciò che precede il periodo (parte intera e antiperiodo):
85 – 8 = 77
scrivere, sotto la barra della divisione, un 9 per ogni cifra del periodo e uno 0 per ogni
eventuale cifra dellantiperiodo:
77/9 = 8,5555555…
Esempi:
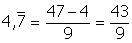
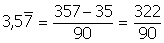
Questa procedura può essere facilmente spiegata utilizzando semplici equazioni di primo grado (
[I1],
[E1],
[F1]
,
[ES1]).
 37/48
37/48

|