|
I numeri razionali - Definizione
Partendo dall’insieme Z dei numeri interi, viene definito l’insieme Q (
[I1],
[I2]
[E1],
[ES1],
[ES2]
,
[F1]
) dei numeri razionali, in modo tale che questo nuovo insieme abbia le seguenti caratteristiche:
sia chiuso rispetto alle operazioni di addizione, moltiplicazione, sottrazione e, a
differenza degli insiemi N e Z, per tutti i numeri diversi da zero, sia anche
chiuso rispetto alla divisione;
tutte le proprietà dell’addizione e della moltiplicazione valide in Z siano valide anche in questo
nuovo insieme.
Per ogni coppia di numeri interi (a,b), con b diverso da zero, definiamo un
nuovo numero
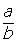
chiamato frazione (
[F1],
[E1],
[ES1],
al quale imponiamo che sia:
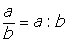
.
I numeri a e b vengono chiamati, rispettivamente, numeratore e
denominatore della frazione.
Le frazioni possono essere interpretate come un’estensione dei numeri interi, in quanto una
frazione del tipo c/1 rappresenta il numero intero c.
Due frazioni a/b e c/d si dicono equivalenti se a*d = b*c.
[E1]
Questa definizione equivale ad affermare la seguente proprietà fondamentale delle frazioni:
Proprietà invariantiva: il valore di una frazione non cambia se numeratore e denominatore
vengono moltiplicati o divisi per uno stesso numero intero diverso da zero.
Esempio:
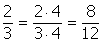
Quando numeratore e denominatore sono primi tra loro, si dice che la frazione è ridotta ai
minimi termini.
La proprietà invariantiva garantisce la possibilità di scrivere un numero illimitato di frazioni
equivalenti ad una frazione data. Questo significa che a partire da una frazione data è possibile
costruire un insieme di infinite frazioni che individuano la stessa quantità.
Introduciamo ora nell’insieme Z x Z-{0} (in alcuni testi si considera, in modo del tutto
equivalente, l’insieme Z x N-{0}) la relazione così definita:
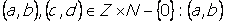 se e solo se a/b è equivalente a c/d.
se e solo se a/b è equivalente a c/d.
E’ facile dimostrare che si tratta di una relazione di equivalenza (
[I1],
[F1]).
L’insieme dei numeri razionali Q è definito come l’insieme che ha per elementi le classi di
equivalenza.
 35/48
35/48

|