Il Teorema più importante della teoria di base dell'insieme dei numeri naturali è anche noto con il nome di principio di induzione, che è una conseguenza immediata del quinto assioma di Peano. Il Principio di induzione fornisce uno strumento molto utile che permette di dimostrare che una certa proprietà P(n)che dipende dai numeri naturali è vera.

L'idea su cui si basa il principio è la seguente:

dimostrare che è vera P(0) e che è vera l'implicazione P(n) 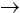P(s(n)); in altre parole va controllata la verità della proprietà P per il numero 0, ed in un secondo momento va dimostrata l'implicazione P(n) 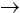P(s(n)), ovvero va dimostrato che supponendo P(n) vera si ottiene che anche P(s(n)) è vera. In tal modo si ha la seguente catena: P(0) vera, allora P(1) vera, allora P(2) vera, allora P(3) vera, ecc. e, in linea di principio, continuando all'infinito si ha la verità di P per ogni numero naturale.

Teorema (Principio di induzione):

Sia P(n) una proprietà dipendente da n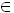N . Si supponga che P(0) sia vera e che P(n)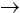P(s(n)) per ogni n naturale; allora si ha che P(n) è vera per ogni 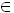nN.