il numero naturale c ottenuto sommando tanti addendi uguali ad a quante sono le unità di b , se b > 1, in simboli a·b=a+a+a+……+a per b volte

il numero naturale 0 se b =0, in simboli a ·0=0

il numero naturale a se b =1, in simboli a ·1= a

Esempio:

2 · 4=2+2+2+2
5 · 0=0
8 · 1=8

L'operazione con la quale, dati due numeri naturali, si trova il loro prodotto è detta moltiplicazione:

• a e b sono detti fattori
• il simbolo dell'operazione è · oppure x

L'operazione di moltiplicazione gode di proprietà analoghe [I1] [E1] [F1] [ES1] :

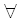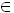1) proprietà commutativa del prodotto: Per a,bN:

a·b=b·a

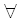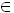2) proprietà associativa del prodotto: Per a,b,cN:

(a·b)·c=(c·a)·b

3) esistenza dell' elemento neutro:; l'elemento neutro per l'addizione è il numero 1, infatti per esso vale:

Per 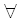a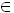N: a · 1 = a

4) Legge di annullamento del prodotto:

Il prodotto di due numeri naturali è zero se e solo se almeno uno dei due fattori è zero:

a·b=0 se e solo se a=0 oppure b=0.

Inoltre abbiamo la seguente proprietà che lega somma e prodotto:

5) proprietà distributiva del prodotto rispetto alla somma:

(a+b)·c = a·c + b·c

Le operazioni elementari che risultano ben definite nell' insieme dei numeri naturali sono l'operazione di addizione (o somma) e quella di moltiplicazione (o prodotto):

a+b = c a·b = f