Le operazioni della sottrazione e della divisione nell' insieme dei numeri naturali non sono sempre fattibili. Esse non sono vere e proprie operazioni in N, cioè non sono funzioni definite da N x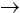 N
N
Vediamo come si definisce la sottrazione di due numeri naturali, è l'operazione inversa della somma:
Definizione: [I1] [E1] [F1] Dati due numeri naturali n,m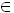
N , si dice n - m quel numero naturale x, se esiste, che sommato ad m dia n. Cioè :
n - m = x se e solo se n = m + x .
Si vede facilmente che n deve essere più grande di m per poter fare l'operazione di sottrazione (cioè perché esista).
La sottrazione è l'operazione indicata con a-b [E1] dove:
- a è detto minuendo, b è detto sottraendo
- il simbolo dell'operazione di sottrazione è –
Nell'insieme N l'operazione di sottrazione è possibile solo se il minuendo è maggiore del sottraendo.
Quando la sottrazione è possibile valgono le seguenti proprietà:
1) Proprietà invariantiva della sottrazione rispetto all'addizione
La differenza di due numeri naturali a e b non cambia se al minuendo e al sottraendo si aggiunge lo stesso numero. La proprietà vale anche se si sottrae al minuendo e al sottraendo uno stesso numero minore o uguale al sottraendo.
12-5=(12+2)-(5+2)=14-7=7
2) Proprietà distributiva della moltiplicazione rispetto alla sottrazione
Il prodotto di un numero naturale per una differenza indicata è pari alla differenza dei prodotti che si ottengono moltiplicando il numero per ciascun termine della differenza:
2·(7-3)=2·7-2·3=14-6=8
(7-3)·2=7·2-3·2=14-6=8
