|
I numeri interi relativi - Definizione
L'insieme dei numeri interi, Z [I1] [I2] [I3] [F1] [E1] [ES1] (dal tedesco
Zahl = numero) può essere definito in modi diversi:
1. Ottenuto da N 'aggiungendo' ad esso una 'nuova copia' dei numeri 1,2,3,... che però si distingue da quella precedente per
quel segno '-' posto in fronte ad essi; possiamo pensarli come numeri 'rossi' se ci immaginiamo un conto in banca: infatti il
primo uso dei numeri negativi è quello di rappresentare dei debiti (già in papiri egizi si trovano numeri che hanno questo
significato).
2. Ottenuto graficamente, come completamento della semiretta dei numeri naturali, facendo una simmetria [I1] [F1] [E1] [ES1] della stessa rispetto ad una retta a questa
perpendicolare, passante per lo 0.
3. Ottenuto partendo da N x N introducendo la relazione di equivalenza ~ [F1] [E1] [ES1], così definita:
(a,b),(c,d) 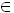 N x N: (a,b) ~ (c,d) se e solo se a + d = b + c.
Si ottiene che Z è l'insieme quoziente N x N/~, cioè l'insieme che ha per elementi le classi di equivalenza. N x N: (a,b) ~ (c,d) se e solo se a + d = b + c.
Si ottiene che Z è l'insieme quoziente N x N/~, cioè l'insieme che ha per elementi le classi di equivalenza.
Nomenclatura:
• I numeri naturali preceduti dal segno + si dicono interi positivi.
• I numeri interi preceduti dal segno - si dicono interi negativi.
• Tutti gli interi positivi appartengono a un insieme detto insieme degli interi positivi.
• Tutti gli interi negativi appartengono a un insieme detto insieme degli interi negativi.
• I due insiemi uniti, più lo zero, costituiscono l'insieme dei numeri interi relativi.
• In simboli: Z+UZ–U {0} = Z
 22/48
22/48

|