|
applicazione del primo principio della termodinamica ai gas perfetti
Poniamo il seguente quesito: come dipende l’energia interna U -per un gas perfetto- dalle variabili di stato T,p e V?
Scegliamo T e V come variabili indipendenti. Come e’ noto, l’equazione di stato dei gas e’ data da:
pV=Nrt
Consideriamo, all’interno di un calorimetro (tipicamente un bagno di acqua di grandi dimensioni), due recipienti A e B collegati da un rubinetto; e supponiamo che all’inizio il gas perfetto sia contenuto in A mentre in B c’e’ il vuoto. Raggiunto l’equilibrio termico, il Joule apre il rubinetto. Che cosa succede? Sicuramente a causa di una depressione, una parte del gas passa da A a B fino a quando si ha l’equilibrio delle pressioni nei due recipienti. Durante, questo movimento di gas, il termometro segna sempre la stessa temperatura, per cui non c’e’ stato uno scambio di calore fra i recipienti e acqua.
Applicando il primo principio della termodinamica al sistema A+B, si ha:
∆U+L=0
Siccome, pero’ il volume di A+B non varia durante la trasformazione, allora risulta L=0 e quindi:
∆U=0
Se –ora- fissiamo la nostra attenzione sul gas, possiamo osservare che il suo volume e’ variato da VA a VA+B mentre T e U non sono variati. Di qui deduciamo che U=U(T)! Determiniamo la sua espressione analitica. Sperimentalmente si dimostra che il calore molare C VV di un gas perfetto non dipende dalla T. Dunque, dalla relazione:
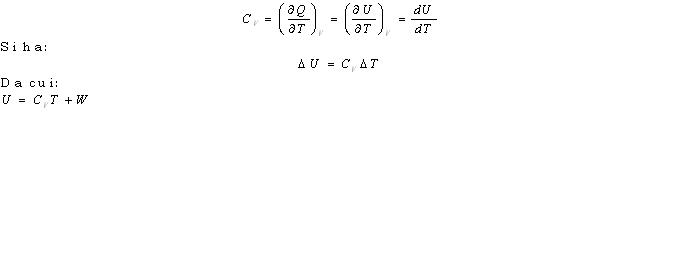
 34/57
34/57

|