|
L'equilibrio alla rotazione
Se pensiamo invece alla rotazione, il discorso è un po'
più complesso.
Consideriamo un corpo esteso, come quello rappresentato in Figura,
sottoposto a forze in grado di farlo ruotare attorno al vincolo O.
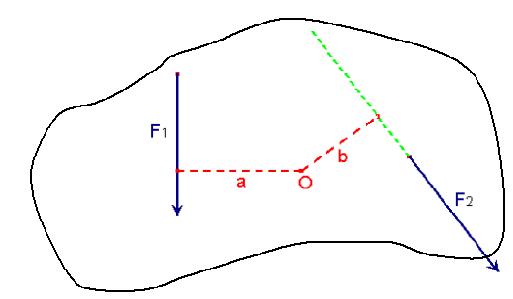
Per avere equilibrio alla rotazione deve essere verificata la seguente
relazione:
F1 a = F2 b
(1)
dove a e b rappresentano le distanze delle forze dal punto O attorno a
cui può ruotare il corpo; queste distanze si chiamano bracci
delle forze rispetto al punto O, mentre i due prodotti F1×a
e
F2×b
si chiamano momenti delle forze rispetto al punto O
([IT],
[ENG],
[FR],
[ES]).
Bisogna notare bene che il braccio di una forza è
individuato dalla distanza tra il vincolo e la retta d'azione della
forza (quello che in matematica è chiamato
distanza tra un punto e una retta ed è dato dal segmento
perpendicolare alla retta passante per il punto) e non è la
distanza tra il punto di vincolo ed il punto di applicazione della
forza.
In generale, il momento di una forza rispetto a un punto è
così definito:
M = F b
dove F è
l'intensità della forza e b il braccio
della forza stessa. Quindi la rotazione provocata da una
forza
è proporzionale non solo alla sua intensità, ma
anche alla distanza della sua retta d'azione dal punto attorno a cui il
corpo può ruotare.
Sono considerati positivi i momenti che tendono a far ruotare il corpo
in senso antiorario (come ad esempio quello della forza F1
della
figura) e negativi quelli che tendono a far ruotare il corpo in senso
orario (come quello della forza F2).
E' noto a tutti gli studenti che per aprire un pesante cancello senza
faticare troppo, bisogna spingerlo o tirarlo alla sua
estremità e non certamente in prossimità dei
cardini! Per lo stesso motivo le maniglie delle porte sono poste
all'estremità opposta rispetto ai cardini (che sono i
vincoli); infatti in questo modo si rende il braccio della forza da noi
applicata per aprire la porta, il più lungo possibile e la
nostra forza risulta essere decisamente più piccola rispetto
a quella che si dovrebbe applicare in prossimità dei cardini.
In base a queste considerazioni, potremo scrivere la relazione (1) nel
modo seguente, più sintetico:
M1=M2,
cioè
M1-M2=0, ovvero
SM=0.
Questa è l'equazione che esprime la condizione di equilibrio
alla rotazione su di un piano. Quindi affinché un corpo non
ruoti, la somma algebrica dei momenti delle forze agenti sul corpo deve
essere nulla.
Nel prossimo paragrafo vediamo come sommare forze parallele.
 20/39
20/39

|