Somma di forze parallele

I casi esaminati sinora però non contemplano il caso in cui le forze agenti sul corpo siano almeno due e parallele. Infatti la condizione di equilibrio, quando le forze agenti sono parallele, si ottiene :

applicando una forza equilibrante che sia uguale ma opposta alla risultante delle forze agenti (è l’equilibrio rispetto alla traslazione) applicando un momento uguale ma opposto a quello esercitato dalle forze agenti (è l’equilibrio rispetto alla rotazione).

Quindi è indispensabile essere in grado di calcolare la risultante delle forze agenti, per sapere dove e quale forza equilibrante applicare.

Per scoprire come sommare forze parallele, si può prendere una gruccia di fil di ferro (in modo che la massa della gruccia si possa considerare trascurabile), con l’estremità inferiore rivestita di carta. Si appende per il suo gancio e si segna sulla carta il punto dove la verticale condotta dal punto di sospensione O a terra incontra l’estremità inferiore. In queste condizioni la gruccia è in equilibrio, perché la forza peso, che pensiamo applicata nel punto individuato in questo modo, è esattamente equilibrata dalla reazione vincolare   applicata al gancio nel punto di sospensione, ossia il sistema è in equilibrio traslazionale poiché la loro risultante è nulla. Analogamente possiamo dire che, poiché il momento di rispetto a O è nullo (dato che il braccio è nullo), il sistema è in equilibrio rotazionale.

In simboli:
P  + V  = 0
M (di P rispetto a O) = 0.

Poi indichiamo sulla carta, a partire da questo punto centrale, una scala graduata in cm. Appendiamo alle estremità dei pesi: per ristabilire l’equilibrio, se applico la forza peso relativa alla massa m₁ ad un’estremità (A), devo applicare la forza peso della massa m₂ = m₁ all’altra estremità (B).

Questo risulta evidente, ma perché bisogna far così?

Cerchiamo di interpretarlo alla luce di forze, momenti e vincoli. La reazione vincolare in O impedisce alla gruccia di precipitare a terra (è quello che chiamiamo equilibrio traslazionale), ma, quando appendiamo la massa m1, in A viene esercitata una forza (peso) diretta lungo la verticale e il cui verso punta verso il suolo: come risultato la gruccia ruota attorno al punto vincolato (O). La forza peso esercitata sulla massa m2 ripristina l’equilibrio rispetto alla rotazione della gruccia attorno ad O. Per interpretarlo bisogna in realtà far ricorso al concetto di momento di una forza rispetto ad un polo O.
 

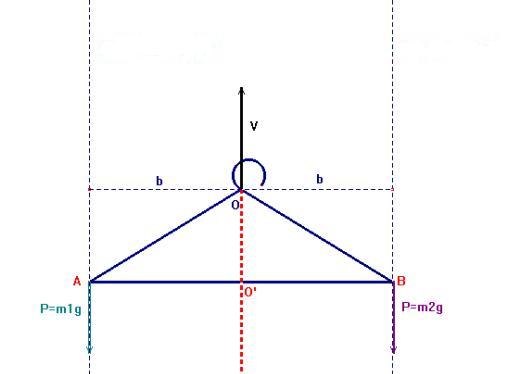
Schema della gruccia in equilibrio con m1=m2

Abbiamo indicato con b il braccio della forza peso della massa m₁ e della massa m₂. Poiché il momento di una forza è definito come il prodotto del braccio per la forza (M=b*F), essendo uguali braccio e forza sia su A sia su B, i due momenti sono uguali (MA = MB), e quindi si ottiene l’equilibrio rispetto alla rotazione. Inoltre, se pensiamo che  faccia equilibrio alla risultante delle due forze peso (P = P₁ + P₂), la risultante delle forze peso, parallele ed uguali in verso e modulo, risulta applicata in O’, cioè equidistante da A e da B (equilibrio rispetto alla traslazione verticale). Quindi abbiamo già ottenuto che la risultante della somma vettoriale di due forze parallele, di uguale modulo e verso, si trova sulla retta equidistante dalle due rette d’azione delle forze che stiamo sommando, e ha lo stesso verso delle forze in questione e modulo pari al doppio del modulo delle medesime forze (si può facilmente verificare grazie a un dinamometro che svolge il ruolo di V).
 
Si può continuare l’attività considerando forze con versi concordi, ma variando uno dei due moduli. Che cosa accade?

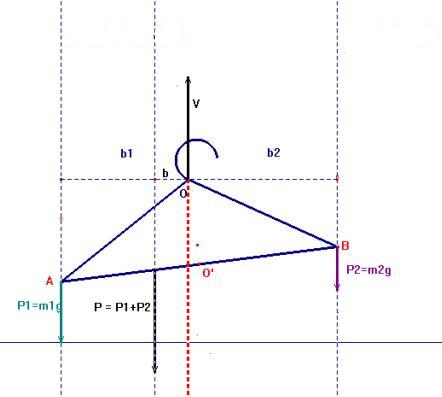
Schema della gruccia non in equilibrio con m1>m2

Evidentemente la gruccia non è più orizzontale, perché ‘pende’ dall’estremità dove è applicata la forza peso maggiore.
Dal punto di vista dei momenti:
M₁ = b₁*P₁
M₂ = b₂*P₂

Nel momento in cui il sistema ha ripristinato l’equilibrio, si ha M₁ = M₂; per fare ciò, il sistema ha dovuto effettuare una rotazione (in senso antiorario, in questo caso) attorno al suo punto vincolato.
Dal punto di vista della risultante P e della reazione vincolare V, possiamo condurre il discorso in questi termini:
durante la rotazione il momento della risultante P rispetto al polo O è non nullo, poiché la risultante P e la reazione vincolare V (applicata in O) non giacciono sulla stessa retta, ma su due rette parallele distanti b (braccio della coppia o braccio di P rispetto ad O). Per avere l’equilibrio bisogna far sì che la risultante P giaccia sulla stessa retta della reazione vincolare V (in questo modo b=0 e il momento rotazionale diventa nullo).
Per fare questo si può lavorare in due modi:

1.  attendere che il sistema ruoti a sufficienza e sovrapponga le due rette d’azione;
2.  spostare il punto in cui applichiamo la forza peso P₁ verso O’ (cioè verso la retta d’azione di V) di un tratto proprio pari a b: in questo caso si ripristina anche la posizione orizzontale della gruccia.

 

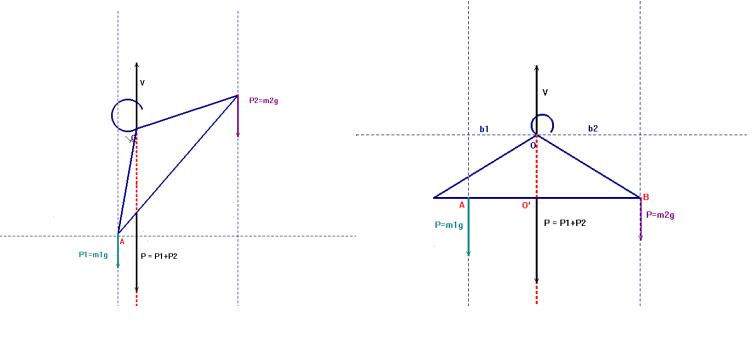
Figura che rappresenta l’equilibrio della gruccia con retta d’azione di P sovrapposta a quella di V senza spostare P1 (a sinistra) e spostando P1 (a destra).

Quindi la risultante della somma di due forze parallele, di uguale verso ma modulo differente, giace su una retta parallela alle altre due, compresa fra di queste e spostata verso la forza di modulo maggiore.
Come possiamo calcolare questo braccio b o, al limite, le distanze tra la retta d’azione della risultante e le rette delle due forze peso applicate?
Possiamo effettuare qualche misurazione col nostro apparato, per cercare di ricavare tale legge. Nell’esperienza che effettuiamo trascureremo la massa della gruccia in quanto molto minore delle masse applicate.
Predisponiamo una tabella di questo tipo:

Massa 1 (g)	Peso 1 (N)	Braccio 1 (cm)	Massa 2 (g)	Peso 2 (N)	Braccio 2 (cm)	P1/P2	b2/b1
139	1,36	3,5	26	0,25	20	5,35	5,71
139	1,36	11,5	76	0,74	20	1,83	1,74
76	0,74	5	26	0,25	15	2,92	3,00
…			…

Qui sono stati riportati i dati di alcune letture effettuate in corrispondenza dei valori delle masse appese, dalle quali è facile ricavare le forze peso applicate, e dei relativi bracci all’equilibrio in posizione orizzontale.
Vediamo così che il rapporto della forza peso P₁ e della forza peso P₂ è pressappoco uguale all’inverso del rapporto dei loro bracci.

Infatti, per avere equilibrio,
M₁ = M₂,    cioè    b₁*P₁ = b₂*P₂.

Ma questo può essere scritto anche così:
P₁/P₂ = b₂/b₁,

cioè la distanza di due forze (parallele ed equiverse) dalla loro risultante è inversamente proporzionale all’intensità delle forze (questa attività è presentata nella seguente applet java [FR]).

Questa che abbiamo ricavato in realtà è la legge con cui lavora la leva, ed era già nota ad Archimede [ENG]; [ES] [IT] ; [FR] 

Un ulteriore passo in avanti deve essere compiuto per stabilire come sommare forze parallele ma di verso opposto. Anche in questo caso, con un apparato tipo quello riportato nella figura sottostante, si può giungere alla conclusione che la risultante R di due forze parallele ma di verso contrario è una forza parallela alle due forze in questione, il cui modulo è pari alla differenza fra i moduli delle due forze, verso concorde con la forza di modulo maggiore e posizionata all’esterno delle due forze, dalla parte di quella di modulo maggiore.


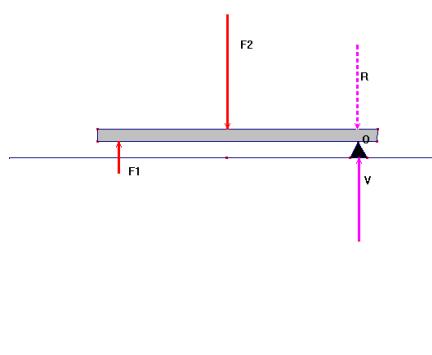
Forze parallele con verso opposto

Un caso notevole di forze parallele ed opposte è quello in cui le forze hanno la stessa intensità. Si parla in questo caso infatti di coppia di forze [FR]; la distanza b fra le rette d’azione è detto braccio della coppia e il momento della coppia è semplicemente M = b*F. Quello che è importante notare è che una coppia di forze dà luogo solo a rotazione, non a traslazione, perché la sua risultante è nulla (F = F₁ - F₂, ma F₁ = F₂).


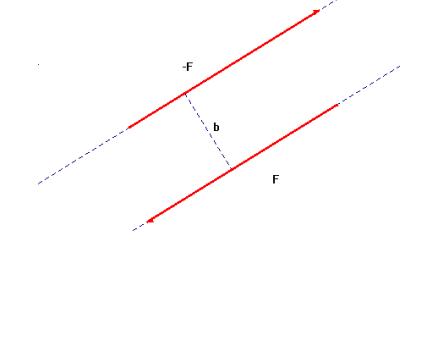
Coppia di forze

   21/39   

Approfondimenti/commenti:

Nessuna voce inserita

Inserisci approfondimento/commento