|
L'equilibrio alla traslazione
Consideriamo un corpo rigido sottoposto a un numero di
forze qualsiasi: resterà in quiete solo se non
potrà né traslare né ruotare. Per
semplicità parleremo di movimenti dovuti a forze complanari
(in due dimensioni, cioè), ma i risultati sono facilmente
estensibili anche al caso tridimensionale.
Se pensiamo alla traslazione, le condizioni affinché il
corpo non trasli sono facilmente esprimibili in questi termini: ogni
movimento traslatorio può essere pensato come somma di due
movimenti lungo due direzioni qualsiasi; scegliamo come direzioni due
direzioni perpendicolari, l'asse x e l'asse y. In questo caso, se il
corpo è in quiete, non può spostarsi
né lungo x né lungo y.
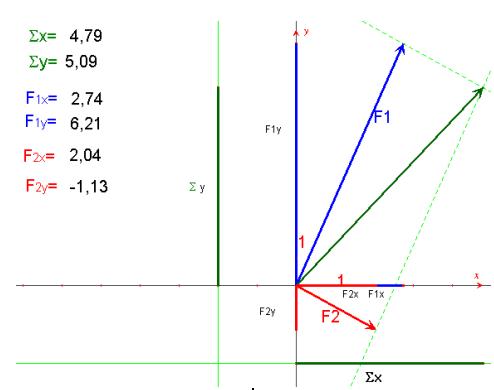
Risultante di due forze.
Perché ciò avvenga deve essere nulla la
risultante delle forze agenti sul corpo. Se indichiamo con Sx la somma
algebrica delle componenti delle forze agenti lungo l'asse x e con Sy
l'omologa lungo l'asse y, diremo che l'equilibrio rispetto alla
traslazione si ottiene chiedendo che: Sx = 0 e Sy = 0. In effetti, se
queste somme sono nulle, un corpo non può mettersi in
movimento né lungo x né lungo y,
perché non esiste forza applicata lungo queste direzioni.
(la seguenti applet java illustra come ricavare la risultante di due o
più vettori [FR]
:
Ricordiamoci però che:
· tra le forze agenti su un corpo vanno considerate anche le
reazioni vincolari, cioè quelle forze che nascono a causa
della presenza di vincoli che limitano i movimenti del corpo in oggetto;
· chiamiamo forza equilibrante la forza in grado di
mantenere in equilibrio il sistema di forze considerato,
cioè la forza uguale e contraria alla risultante!
Mantenere in sospensione un oggetto tramite una fune è un
classico esempio di equilibrio rispetto alla traslazione: la forza
equilibrante è il vincolo della fune, che si oppone alla
forza peso agente sul corpo.
 19/39
19/39

|