|
Il XX secolo: i modelli atomici - concezione moderna
5.1 Niels Bohr
Essendo sorte diverse questioni circa il modello di Rutherford ci si chiedeva se si dovesse abbandonare tale modello, ma questo non era giustificabile dal momento che, per i fenomeni che si sono visti, il modello si presentava perfettamente valido, oppure rinunciare alle leggi classiche della meccanica e dell'elettromagnetismo.
In questo secondo caso si stava verificando una frattura che in un altro momento storico la scienza aveva sanato. Cioè: la teoria della gravitazione aveva eliminato con Newton la scissione, di derivazione aristotelica, tra fisica celeste e fisica terrestre; ora lo studio del microcosmo atomico riproponeva una frattura tra leggi macroscopiche e leggi atomiche. Il matrimonio fu realizzato da Niels Bohr.
Nel 1911 giunse a Manchester il giovane fisico danese Niels Bohr (aveva all'epoca 25 anni). A quel tempo Rutherford stava già preparando i suoi storici esperimenti che lo portarono a formulare la teoria del nucleo atomico [En]
[F]. Bohr apprezzava le idee di Rutherford, il quale a sua volta lo stimava notevolmente. La teoria di Bohr sulla struttura dell'atomo fu pubblicata nel 1913 e si basò sulla scoperta di Rutherford, secondo la quale gli atomi sono simili a sistemi planetari.
La prima difficoltà incontrata da Bohr in questo quadro era che gli atomi avrebbero potuto esistere solo per una piccolissima frazione di secondo. Infatti un elettrone in moto su una data orbita è equivalente a un oscillatore elettrico ed è quindi costretto a emettere onde elettromagnetiche perdendo rapidamente energia. Si può facilmente dimostrare che in conseguenza di questo fatto gli elettroni atomici si muoverebbero su traiettorie a spirale terminando la loro corsa sul nucleo in un tempo dell'ordine di 10-8 s. Certamente però le cose andavano diversamente dal momento che gli atomi risultavano possedere configurazioni assai stabili.
5.2 La soluzione proposta da Bohr
La situazione si presentava alquanto paradossale, un po' come la catastrofe ultravioletta [En]
[F]
paventata da Jeans, e Bohr pensò che la soluzione di questa difficoltà si dovesse ricercare sulle stesse linee di quella. Se l'energia radiante poteva esistere solo in certe quantità minime o in multipli di queste quantità, perché non far la stessa ipotesi sull'energia meccanica degli elettroni ruotanti intorno al nucleo? In questo caso il moto degli elettroni nello stato fondamentale di un atomo corrisponderebbe a queste minime quantità di energia, mentre gli stati eccitati corrisponderebbero a un maggior numero di questi quanti di energia meccanica. Un meccanismo atomico dovrebbe comportarsi, da questo punto di vista, come la leva del cambio di un'automobile : la si può inserire in prima, in seconda, in terza e così via, ma non in una posizione intermedia. Se il moto degli elettroni atomici e la luce emessa da questi vengono entrambi quantizzati, allora la transizione di un elettrone da un livello quantico più elevato a uno più basso all'interno di un atomo provoca l'emissione di un quanto di luce di energia hf uguale alla differenza di energia tra i due livelli; inversamente, se l'energia hf di un quanto di luce incidente è uguale alla differenza di energia tra lo stato fondamentale e lo stato eccitato, il quanto sarà assorbito da un elettrone, il quale subirà una transizione da uno stato più basso a uno più alto.
Questi scambi energetici tra materia e radiazione sono schematicamente illustrati nella figura seguente.
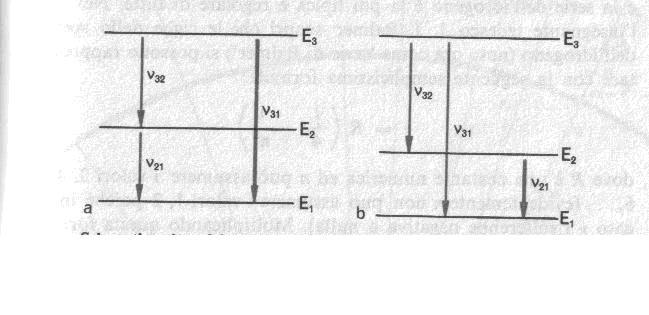
Schematizzazione del principio di Rydberg. a) Se un elettrone può saltare dal livello energetico E3 al livello energetico E2 emettendo un quanto di luce di frequenza f32 e dal livello energetico E2 al livello energetico E1 emettendo un quanto di frequenza f21, deve essere possibile la transizione diretta dal livello E3 al livello E1 con emissione di un quanto di frequenza f31 = f32 + f21. b) Se un elettrone può saltare dal livello E3 al livello E2 emettendo un quanto di frequenza f32 e dal livello E3 al livello E1 emettendo un quanto di frequenza f31, dev’essere possibile anche la transizione diretta dal livello E2 al livello E1 e quindi l’emissione di un quanto avente frequenza f21 = f31 - f32.
Osservandola possiamo giungere a un'importante conclusione. Se un quanto di luce di energia hf32 può essere emesso quando un elettrone passa dallo stato a energia E3 allo stato a energia E2, e analogamente un quanto di luce di energia hf21 può essere emesso quando un elettrone passa dallo stato a energia E2 allo stato a energia E1, si dovrebbe osservare, almeno in alcuni casi, anche un quanto di luce di energia
hf32+ hf21 = h(f32+ f21) = hf31,
cioè una transizione diretta dallo stato E3 allo stato E1.
Analogamente l'emissione di un quanto di luce di energia hf31 e di uno di energia hf32 indica la possibilità di emissione di un quanto di energia
hf31 - hf32 = h(f32 - f32) = hf21.
A parte il fattore costante h, si può affermare che se in uno spettro compaiono due righe di emissione aventi certe frequenze, nello stesso spettro devono comparire anche le righe corrispondenti alla somma delle due frequenze e alla loro differenza. Questo è il cosiddetto 'principio di combinazione di Rydberg', scoperto empiricamente dallo spettroscopista tedesco Rydberg [En] molto
tempo prima della nascita della teoria dei quanti.
Tutti i fatti descritti non lasciavano alcun dubbio sulla correttezza della teoria formulata da Bohr sulla quantizzazione dell'energia meccanica, ma restavano da scoprire le regole di tale quantizzazione. A questo scopo Bohr analizzò il più semplice atomo esistente: l'atomo d'idrogeno, costituito da un solo elettrone che ruota attorno ad un nucleo costituito da un'unica carica elettrica positiva, il protone [F], [I].
5.3 Lo spettro dell'atomo d'idrogeno
Lo spettro visibile dell'idrogeno contiene quattro righe: una rossa, una blu e due violette, ma l'esame di tale spettro nella regione ultravioletta mise in evidenza l'esistenza di un gran numero di righe di lunghezza d'onda minore [F], [Es] . Successioni di righe spettrali che si affollano sempre più fittamente verso un limite definito dalla parte delle alte frequenze erano note in spettroscopia come serie e la serie dell'idrogeno è la più tipica e regolare di tutte. Nel 1885 l'insegnate tedesco Balmer scoprì che le righe dello spettro dell'atomo d'idrogeno (note come 'serie di Balmer') si possono rappresentare con la seguente formula:
f = R(1/4 - 1/n2)
dove R è una costante numerica ed n può assumere i valori numerici 3,4,5...(non 1 e 2, perché altrimenti la frequenza diventa negativa). Moltiplicando per h (costante di Planck [F1], [F2] ), in modo da ottenere l'energia del quanto di luce emesso nella transizione, si ha:
hf = hR(1/4 - 1/n2)
che Bohr riscrisse così:
hf = hR(1/22 - 1/n2)
Segue che il termine - hR /n2 dovrebbe rappresentare i livelli energetici dell'elettrone in un atomo d'idrogeno tra i quali avvengono le transizioni corrispondenti all'emissione delle righe di Balmer. Il segno - indica che l'energia orbitale di un elettrone in un atomo è negativa, intendendo con ciò dire che la loro energia cinetica è minore dell'energia potenziale del campo elettrico e impedisce loro di uscire dall'atomo. Che tipo di moto attorno al nucleo corrisponde a questi valori dell'energia?
Per rispondere basta ricordare che l'energia potenziale delle forze di Coulomb varia in modo inversamente proporzionale alla distanza dal centro. Poiché i termini della serie di Balmer variano come l'inverso del numero intero n, è evidente che i raggi delle orbite quantiche successive devono aumentare come n2.
Le transizioni elettroniche dalle orbite più esterne alla seconda orbita (n=2) corrispondono alle righe della serie di Balmer, ma quali sono le altre possibilità? Le transizioni dalle orbite 2,3,4,... alla prima orbita devono costituire una serie di righe simile alla serie di Balmer, ma posta nell'estrema regione ultravioletta dello spettro; non solo, ma le transizioni dalle orbite più esterne all'orbita 3 devono formare una serie nell'estrema regione infrarossa. Entrambe le serie furono scoperte poco dopo dagli spettroscopisti Theodore Lyman e Friederich Paschen e la loro comprovata esistenza diede un notevole sostegno alla teoria di Bohr sulle transizioni degli elettroni.
Infatti Bohr, sapendo che i raggi delle orbite quantiche (supposte circolari) aumentano con i quadrati dei numeri interi, fu in grado di stabilire quale grandezza meccanica fosse 'quantizzata', cioè aumentasse di una quantità fissa da un'orbita all'altra. Risultò che questa grandezza è il prodotto della quantità di moto dell'elettrone per la lunghezza della circonferenza dell'orbita, quantità nota in meccanica classica col nome di azione.
Inoltre la variazione dell'azione nel passaggio da un'orbita all'altra risultò proprio uguale alla costante h, introdotta da Planck nella sua teoria della radiazione termica e da Einstein nella sua interpretazione dell'effetto fotoelettrico [F]
[Es] .
La teoria di Bohr nel primo decennio successivo alla sua formulazione portò a notevoli successi nell'interpretazione degli atomi complessi, dei loro spettri ottici e delle interazioni chimiche; ma, nonostante tutto, essa manteneva la sua originaria natura scheletrica e tutti i tentativi di descrivere in particolare le transizioni elettroniche da uno stato energetico all'altro e di calcolare le intensità delle righe spettrali emesse durante queste transizioni non portavano molto lontano.
5.4 Il modello atomico con le orbite "quantizzate"
Riassumendo, con Bohr il modello di Rutherford subiva quattro modifiche essenziali: prima di tutto, per rispettare l'ipotesi di partenza, l'elettrone non può ruotare intorno al nucleo su orbite qualsiasi ma su orbite fisse privilegiate, corrispondenti ai vari livelli di energia; in secondo luogo, se l'elettrone persiste nel ruotare su queste orbite privilegiate non emette energia; terzo, l'elettrone può saltare spontaneamente da un livello all'altro; infine, la frequenza della radiazione emessa o assorbita nel salto è legata al "quanto" da una certa formula.
Quindi un elettrone che ruota intorno ad un nucleo deve rispettare certe particolari condizioni dinamiche ed energetiche; questi limiti si possono riassumere in due teoremi:
- un elettrone può descrivere intorno al nucleo solo una successione discreta di orbite, nel senso che non tutte le orbite sono permesse (quantizzazione delle orbite)
- quando un elettrone percorre una data orbita in contrasto con le leggi dell'elettromagnetismo non irradia energia. Solo a seguito di una transizione da un orbita ad un'altra si ha una variazione del contenuto energetico dell'atomo (quantizzazione dell'energia)
Bohr era riuscito a rendere conto sul piano teorico di quella stabilità degli atomi che il modello di Rutherford non forniva; in più spiegava anche la costanza degli spettri emessi dalle varie sostanze. Nello spettro si trovano tutte le frequenze consentite per i vari tipi di atomi, perché in ogni atomo gli elettroni si trovano a certi livelli energetici tipici e consentiti per ogni elemento.
La teoria di Bohr, formulata inizialmente per l'atomo più semplice, cioè per l'idrogeno, permise di calcolare teoricamente il valore di una costante già stabilita sperimentalmente dalle ricerche spettroscopiche (costante di Rydberg - costante caratteristica di ciascun elemento, avente le dimensioni dell'inverso di una lunghezza, che interviene nelle serie spettroscopiche, i cui termini danno i numeri d'onda delle radiazioni emesse dall'elemento che si considera) ove e,m sono la carica e la massa dell'elettrone, M è la massa del nucleo, Z è il numero atomico, c è la velocità della luce nel vuoto, h è la costante di Planck.
Tale espressione porta valori numerici:
R=109677,69 cm-1 per l'idrogeno,
(R=109722,40 cm-1 per l'elio, in ottimo accordo con l'esperienza).
I valori così trovati collimavano: un successo di Bohr.
Ma ecco i problemi irrisolti che la teoria di Bohr lasciava:
- non giustificava il mancato irraggiamento degli elettroni costretti a ruotare intorno solo ad alcune orbite
- non dava alcuna informazione sull'intensità delle righe degli idrogenoidi (oltre all'idrogeno sono atomi degli elementi leggeri ionizzati in modo da aver perduto tutti gli elettroni eccetto uno).
Inoltre ci furono difficoltà nell'estendere il modello ai sistemi formati da più di un elettrone : non c'era alcun criterio razionale per ripartire gli elettroni nelle loro orbite.
Apparve presto necessario generalizzare il modello originale di Bohr, a orbite quantiche circolari, aggiungendo qualche orbita ellittica quantizzata. Questa estensione fu dovuta al fisico tedesco Arnold Sommerfeld.
[En]
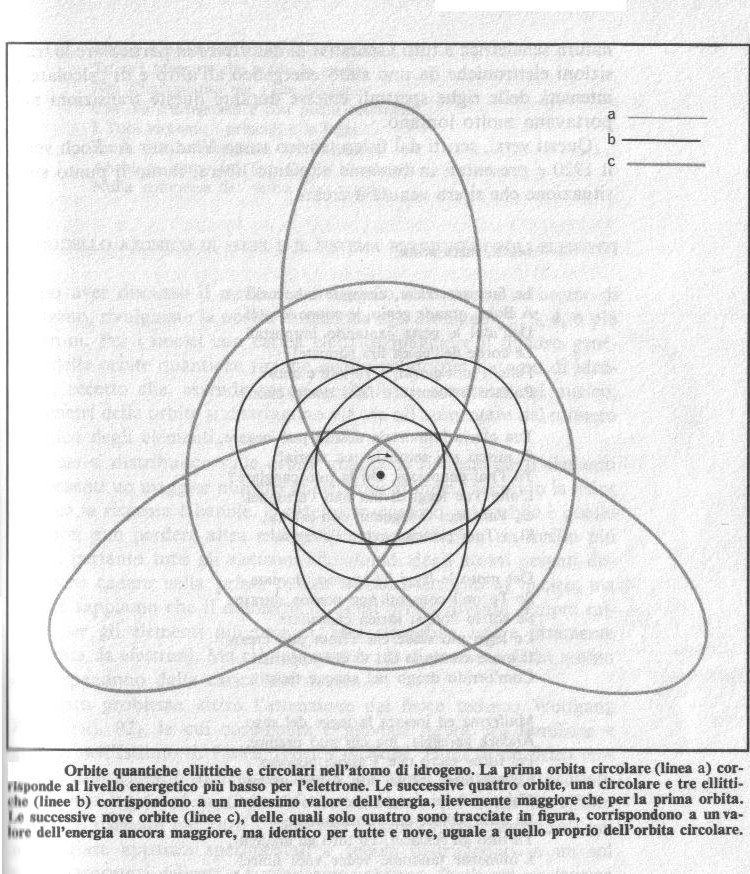
La figura seguente illustra alcuni gruppi di possibili orbite quantiche dell'elettrone nell'atomo d'idrogeno.
5.5 Gli orbitali atomici
Nel 1916, il fisico tedesco Arnold Sommerfeld estese alle orbite ellittiche dell'atomo di idrogeno le ipotesi che Bohr aveva enunciato solamente per le orbite circolari. Questa estensione avvenne mediante l'applicazione ai moti dell'elettrone della meccanica relativistica di Einstein.
La prima orbita circolare restò inalterata (linea più sottile, a). Alla seconda orbita circolare Sommerfeld aggiunse tre orbite ellittiche (linee b), sulle quali l'elettrone aveva la stessa energia che aveva sull'orbita circolare. Alla terza orbita circolare vennero aggiunte otto orbite ellittiche (di cui solo tre sono indicate in figura con le linee c), anch'esse tutte corrispondenti all'energia che l'elettrone possiede nell'orbita circolare. Per gli ordini maggiori il numero delle orbite ellittiche da aggiungere diventava sempre maggiore. La situazione diventava via via più complessa, ma il quadro si adattava sempre meglio alle osservazioni sperimentali. L'atomo non era più un piccolo sistema planetario, nel quale Giove poteva saltare nell'orbita di Venere, ma era dipinto come uno schema astratto solo lontanamente collegabile ai cerchi e alle ellissi della meccanica classica.
Da quest'estensione derivò un'importante conseguenza: Sommerfeld poté rilevare che le orbite ellittiche degli elettroni non sono equidistanti, ma formano dei gruppi (detti strati o anelli) elettronici; le orbite dello stesso strato hanno energie che differiscono fra di loro di valori piccolissimi. Questi strati sono per convenzione identificati con le lettere K, L, M, N, eccetera, partendo dagli strati interni. Gli strati comprendono diversi numeri di orbite che vanno da 2 a 8, a 18, a 32, ecc., a mano a mano che si va verso l'esterno.
5.6 Il momento magnetico dell'elettrone e lo spin
Tutto a questo punto pareva risolto e controllato sperimentalmente. Ma ancora una volta l'atomo sfuggiva alla presa dei fisici: la teoria di Sommerfeld - applicazione delle teorie relativistiche all'atomo di Bohr- non teneva conto di alcuni fatti: non spiegava quantitativamente la complessità degli spettri, che si rivelavano ad esami più attenti ancor più complicati e non rendeva ragione di alcune anomalie magnetiche dell'atomo.
In breve, il modello di Bohr - Sommerfeld non spiegava sufficientemente i processi che avvengono all'interno dell'atomo: quando un elettrone salta da un'orbita all'altra? Per quanto tempo un elettrone persiste in un'orbita? Bohr stesso scrisse: bisognava rinunciare a descrivere il comportamento individuale degli atomi nello spazio e nel tempo, conformemente al principio di causalità, e immaginare che la natura può fare, tra diverse possibilità, una libera scelta che non è sottoposta che a considerazioni di probabilità.
Nel 1917, Albert Einstein [F], [En] introdusse, nello studio dell'atomo di Bohr, alcuni coefficienti di probabilità. Einstein formulò cioè l'ipotesi che un elettrone cambi orbita spontaneamente, cioè senza intervento di cause esterne al sistema dell'atomo.
Se l'atomo viene colpito da una radiazione luminosa con frequenza pari alla frequenza corrispondente ad un salto, l'elettrone compie questo passaggio in un'orbita esterna e lo compie con tanta maggior probabilità quanto maggiore è l'intensità della luce che colpisce l'atomo.
Nel 1925, i fisici Uhlenbeck e Goudsmit, per spiegare alcuni particolari fenomeni degli spettri di emissione e di assorbimento degli atomi e alcuni fatti riguardanti il ferromagnetismo e il paramagnetismo presenti in certe sostanze (non ancora spiegati con la teoria di Bohr), idearono un'altra ipotesi. Uhlenbeck e Goudsmit supposero che ogni elettrone, proprio come fanno i satelliti naturali, oltre che ruotare intorno al nucleo ruoti anche su se stesso. Rivoluzione e rotazione tornavano nella similitudine fra atomo e Sistema Solare. L'elettrone cioè aveva proprietà simili a quelle di un giroscopio [En]
[F], il cui asse, grazie al moto di rotazione intorno all'asse passante per il baricentro, tende a conservare una direzione ben determinata nello spazio. Ma non basta; essendo elettricamente carico, l'elettrone assomiglia ad un piccolissimo magnete. I fisici adottarono il termine spin [En1]
[En2]
[F1]
[F2]
[F3], che in inglese significa appunto rotazione, e qui è sinonimo di momento angolare meccanico; una grandezza fisica che dà una misura della velocità di rotazione della particella e l'indicazione del verso in cui avviene la rotazione stessa.
Lo spin venne trattato da Uhlenbeck e Goudsmit con le stesse leggi quantistiche usate da Bohr per il moto di rivoluzione dell'elettrone e ne dedussero che un elettrone ha sempre lo stesso ben determinato spin, in altri termini ha sempre la stessa velocità di rotazione su se stesso. Altra conclusione ricavata dall'ipotesi dello spin è questa: poiché produce un campo magnetico, l'elettrone può avere l'asse soltanto in due direzioni rispetto al campo magnetico esterno, o la stessa direzione e lo stesso verso del campo esterno, oppure la stessa direzione ma verso opposto (l'elettrone può essere, si dice, o parallelo o antiparallelo).
I valori dedotti dai due fisici a proposito dello spin e del momento magnetico dell'elettrone [En]
permisero di interpretare quantitativamente le proprietà ottiche e magnetiche che non venivano spiegate dal modello atomico di Bohr.
L'ipotesi dell'elettrone ruotante era solo un'immagine, ma rimase per molto tempo una rappresentazione valida anche dal punto di vista teorico. Nel giro di pochi anni, dall'atomo di Rutherford a quello di Bohr-Sommerfeld e a quello di Uhlenbeck e Goudsmit, cioè dal 1911 al 1925, si era passati a una forma più valida di interpretazione; a un modello sempre più complesso che aveva richiesto un lavoro rivoluzionario e ormai ben distante dalla fisica classica.
5.7 Il principio di Pauli
Dopo aver discusso il moto di un singolo elettrone in un atomo di idrogeno, si prendano in considerazione gli atomi con 2,3,4 o più elettroni. Per i nuclei con carica maggiore il quadro generale delle orbite quantiche rimane quello valido per l'atomo di idrogeno, eccetto che, essendo maggiore la forza attrattiva del nucleo, i diametri delle orbite si restringono via via all'aumentare del numero atomico degli elementi. Come si distribuisce sulle orbite quantiche ristrette degli elementi più pesanti un maggior numero di elettroni? Secondo la fisica classica è banale.
Il sistema meccanico più stabile è quello che non può perdere altra energia per transizione in un livello più basso, pertanto tutti gli elettroni addizionali degli atomi pesanti dovrebbero cadere nella prima orbita e rotare intorno al nucleo, ma poiché il diametro di quest'orbita diventa sempre minore per gli elementi più pesanti, essa dovrebbe essere fittamente popolata di elettroni. Ma ciò non accade: le dimensioni di un atomo non dipendono dalla carica del nucleo.
Questo problema attirò l'attenzione del fisico austriaco Wolfgang Pauli [Es], [I].
Studiando il moto degli elettroni all'interno di un atomo, Pauli formulò il principio ora famoso che egli chiamò principio di esclusione, detto anche principio di Pauli [En]
[F1]
[F2], secondo il quale ogni orbita quantica non può contenere più di due elettroni [Es1]
[Es2].
Il principio afferma cioè che, se entrambi i posti su un'orbita sono occupati, i successivi elettroni devono prendere posto in altre orbite. Quando tutte le orbite di un dato strato sono piene, cominciano a riempirsi le orbite dello strato successivo. Quando il principio di Pauli fu formulato si credeva che gli elettroni fossero cariche elettriche negative puntiformi, ma ben presto si scoprì che gli elettroni devono essere pensati anche come piccolissimi magneti; essi infatti posseggono un momento magnetico a causa del moto di rotazione su se stessi mentre ruotano attorno al nucleo. Un elettrone può ruotare su se stesso in due modi : o nello stesso verso di rivoluzione attorno al nucleo o in verso opposto. Si è dimostrato che i due elettroni di un'orbita quantica devono ruotare in senso opposto: tale notevole scoperta portò a nuova formulazione del principio di Pauli, leggermente diversa da quella originale. Il principio di esclusione di Pauli asserisce che più particelle identiche di spin n + 1/2 (n = 0, 1, 2, 3, ...) non possono assumere lo stesso stato quantico. Poiché la maggior parte delle particelle costituenti la materia hanno spin 1/2 (elettroni, protoni, neutroni, ecc.), questo principio limita fortemente il numero delle possibili configurazioni che può assumere un sistema di particelle identiche del tipo descritto, nel senso che non è possibile trovarne una coppia con gli stessi numeri quantici.
Il principio di esclusione trova la sua giustificazione nelle molteplici conferme sperimentali che ha avuto; l'interpretazione corretta della tavola periodica degli elementi chimici di Mendeleev, la spiegazione di molti fenomeni nucleari sono esempi sufficienti a fissarne l'importanza fondamentale nella fisica moderna.
5.8 De Broglie e la natura ondulatoria della materia
Nel 1924 un aristocratico francese, il marchese Louis de Broglie [En], il quale aveva iniziato la sua carriera scientifica come studioso di storia medioevale e solo più tardi cominciò a nutrire un certo interesse per la fisica teorica, presentò all'Università di Parigi una tesi di laurea contenente delle idee straordinarie. De Broglie riteneva che il moto delle particelle materiali fosse seguito e guidato da certe onde 'pilota' che si propagavano nello spazio insieme alle particelle. In conseguenza di questo fatto le orbite quantiche del modello di Bohr potevano essere interpretate come quelle orbite che soddisfacevano alla condizione di contenere un numero intero di queste onde pilota : un'onda nella prima orbita, due nella seconda, ecc. In precedenza si è visto che, nel caso del moto circolare, le orbite di Bohr devono soddisfare alla condizione che il prodotto della loro lunghezza (2pigreco*r) per la quantità di moto (mv) dell'elettrone mobile sia uguale ad h per la prima orbita, 2h per la seconda, 3h per la terza e così via. Questi due postulati diventano identici se si ammette che lunghezza dell'onda pilota sia uguale ad h divisa per la quantità di moto della particella, cioè lambda = h/mv.
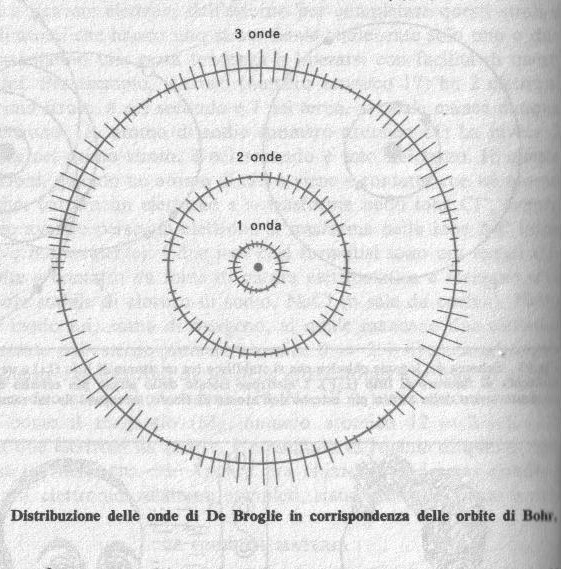
Questa fu appunto l'ipotesi di de Broglie. Per tutte le orbite di raggio intermedio a quello delle orbite quantiche un'onda pilota 'non può prendersi per la coda' e di conseguenza quel tipo di moto non può esistere. In questo modo, con questa audace uscita, de Broglie trasformò le scheletriche orbite di Bohr in un concetto più sostanzioso di canne d'organo, membrane di tamburo, ecc. La meccanica quantistica [F], [Es] delle particelle acquistava per merito di de Broglie proprietà simili a quelle delle onde luminose o sonore.
[En].
Questa proposta rivoluzionaria poteva prestarsi ad un immediato controllo sperimentale: infatti, se fosse stato vero che gli elettroni erano guidati dalle onde di de Broglie nel loro moto atomico, essi dovevano mantenere e mostrare quella proprietà ondulatoria anche quando si muovevano liberamente nello spazio seguendo traiettorie rettilinee. Per i fasci di elettroni di pochi kVolt usati comunemente in laboratorio la lunghezza d'onda di de Broglie avrebbe dovuto essere di circa 10-8 cm, quindi dello stesso ordine di grandezza di quella dei raggi X, cosicché, mediante la tecnica di diffrazione dei raggi X, si sarebbe potuto stabilire se l'ipotesi di de Broglie fosse o meno accettabile.
Un esperimento in questo senso fu eseguito nel 1927 dal figlio di Sir J.J. Thomson, George, e dai fisici americani Davisson e Germer, i quali inviarono su un cristallo un fascio di elettroni accelerati in un campo elettrico. Il risultato ottenuto fu una figura nella quale risultava evidente il fenomeno della diffrazione. Dall'analisi del diametro degli anelli si diffrazione si calcolò che la lunghezza d'onda coincideva esattamente con quella prevista dalla teoria di de Broglie, cioè data da h/mv. Si osservò anche che, accelerando o rallentando il fascio, la lunghezza d'onda diminuiva o aumentava. Pochi anni dopo il fisico tedesco Otto Stern ripetè l'esperimento di Davisson e Germer utilizzando un fascio di atomi di sodio invece di elettroni e trovò che il fenomeno della diffrazione predetto da de Broglie si verificava anche in questo caso.
In questo modo venne confermata la teoria ondulatoria della materia.
 6/6
6/6
|