Nel 17-esimo secolo il matematico olandese Christian Huygens studiò i fenomeni degli urti fra due corpi, scoprendo che per descrivere completamente il moto di un corpo non basta misurarne la sua quantità di moto (q=mv), ma occorre anche un'altra grandezza, che egli chiamò "forza viva" (e che oggi chiamiamo energia cinetica E=1/2mv²) che definì come la proprietà che il corpo acquista quando viene messo in moto, in aggiunta rispetto alla quantità di moto.

Urti tra due masse: energia cinetica [ENG] ; [ES] ; [IT]

Consideriamo due palline: la prima, di massa m₁ è ferma e l'altra, di massa m₂, che si muove con velocità v, la urta. Dopo l'urto la prima pallina, che inizialmente era ferma, avrà una velocità v₁ e la seconda avrà velocità v₂.

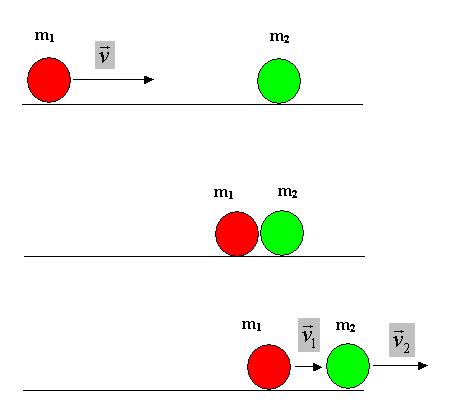
Per descrivere completamente l'urto occorrono due equazioni di conservazione:

m₁v = m₁v₁ + m₂v₂

e

1/2m₁v² = 1/2m₁v²₁ + 1/2m₂v²

L'energia cinetica cambia (così come la quantità di moto), quando alla pallina viene applicata una forza, compiendo così un lavoro. Si ritorna in questo modo al concetto per il quale è tramite il lavoro che viene scambiata energia (cinetica) tra le due palline.

L'energia cinetica viene definità come una proprietà che un corpo acquista quando viene messo in moto e che l'applicazione di una forza può far variare.

Caduta di un grave: energia potenziale [ENG]; [ES] ; [IT]

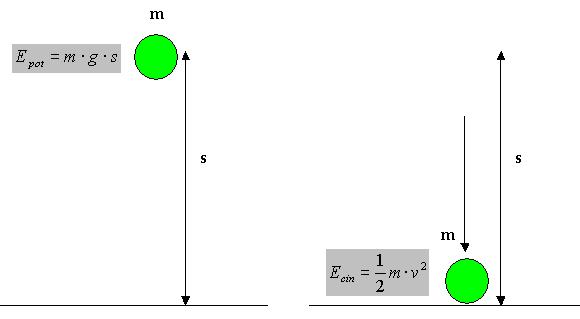
Supponiamo ora di portare la pallina ad una certa altezza s da terra e quindi di lasciarla cadere. La pallina colpirà il terreno dopo un certo tempo (misurabile con un cronometro) ad una velocità v, la cui espressione è data dalle legge di caduta di un grave:

v = gt

dove g è l'accelerazione di gravità, t è il tempo misurato e con un'energia cinetica (massima al momento dell'urto con il suolo):

E = 1/2mv²

Questo semplice esempio porta ad un altro concetto molto importante: man mano che cade la pallina acquista velocità ed energia cinetica, quindi vi è qualcosa che produce un lavoro che, come detto nei paragrafi precedenti, trasferisce energia alla pallina.

Ma che cosa?

Allo stesso modo in cui, nell'esempio della fionda, quando si tirava l'elastico si compiva un lavoro caricando energia che poi veniva trasferita alla pallina quando lo si rilasciava, ora si è caricata energia nella pallina portandola all'altezza s.

Questa energia, dovuta come si intuisce, al fatto che la pallina è stata portata ad una certa altezza s da terra, si chiama energia potenziale.

Ad esempio l'acqua in una diga che sbarra un fiume ad una certa altezza ha una energia potenziale che viene sfruttata quando l'acqua viene fatta cadere in una condotta forzata per produrre energia elettrica, questa energia potenziale, data dalla forza di gravità per l'altezza di caduta, produce un lavoro che trasforma la sua energia potenziale in energia cinetica che poi viene usata per far girare le turbine che la trasformano in energia elettrica.

In accordo con quanto introdotto in precedenza per cui l'energia si trasforma da una forma all'altra, non può crearsi o distruggersi. Lo stesso succede alla pallina, quando viene portata ad altezza s da terra e quindi lasciata cadere. L'energia potenziale è quindi, in questo caso e nel caso della diga, legata all'altezza s, alla accelerazione di gravità g ed alla massa delle pallina (o dell'acqua della diga):

E_pot = m g s

Nel caso della pallina sollevata da terra, in particolare, prende il nome di energia potenziale gravitazionale perchè è sottoposta al campo gravitazionale della Terra.

Nel caso precedente dell'elastico della fionda, quando viene teso l'elastico è accumulata dell'energia potenziale elastica.