|
GRANDEZZE VETTORIALI
Le grandezze fisiche si possono classificare come scalari e vettoriali. Le grandezze scalari [IT24] [IT25] [ES23] [EN24] [EN25]
[FR23]
[FR24]
sono definite tramite un’unità di misura e un numero che ne traduce la misura (intensità della grandezza). Esempi di grandezze scalari sono la massa, il tempo, la temperatura, il lavoro, l’energia, la carica elettrica.
Le grandezze vettoriali sono definite tramite un’unità di misura e un vettore [IT26] [IT27] [ES24] [ES25] [EN26] [EN27]
[FR25]
[FR26]
, ovvero grandezze che per la loro definizione necessitano di direzione, verso e modulo [IT28] [ES26]
[FR27]
. Esempi di grandezze vettoriali sono: velocità, accelerazione, forza [IT29] [ES27] [ES28] [EN28] [EN29]
[FR28]
[FR29]
, campo elettrico.
Il modulo di una grandezza vettoriale indica la misura della grandezza stessa rispetto ad una opportuna unità di misura. Un vettore è rappresentato graficamente da una freccia ed è caratterizzato da direzione, modulo e verso.
- Direzione: è la retta [IT30] [ES29] [EN30] [EN31] su cui giace il vettore;
- Verso: è il verso di percorrenza lungo la retta, indicato dal verso della freccia;
- Modulo: è la lunghezza della freccia;
Un vettore si indica con una lettera in grassetto oppure ponendo una freccetta sopra la lettera, mentre la lettera stessa indica il modulo.
Scomposizione di un vettore
Dato un singolo vettore, trovare due vettori che sommati siano equivalenti ad esso.
Supponiamo che un dato vettore sia rappresentato dalla freccia AB nel disegno. Volendo scomporre il vettore AB:
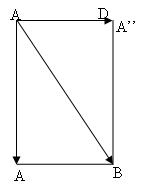
tracciamo due linee lungo AA' e AA" e due linee parallele ad esse che finiscano nel punto B. Se AA' e AA" sono perpendicolari tra loro (che è il caso più usuale), queste linee racchiuderanno un rettangolo ACBD, di cui AB è la diagonale. È ora evidente che AC e CB costituiscono la soluzione del nostro problema, e, con un’addizione di vettori [IT31] [IT32] [ES30] [ES31] [EN32] [EN33]
[FR30]
[FR31]
AC + CB = AB
AC e CB sono chiamate le componenti di AB (o i vettori componenti di AB) lungo le due direzioni assegnate.
Nel caso in cui AA' e AA" non sono perpendicolari, allora il quadrilatero ACBD diventa un parallelogramma.
Esercizi con i vettori
[FR32]
[FR33]
 6/15
6/15

|